References
[1] M. Clerc and J. Kennedy, "The Particle Swarm-Explosion, Stability, and Convergence in a Multidimensional Complex Space," IEEE Transactions on Evolutionary Computation, vol. 6, pp. 58-73, 2002.
[2] J. Kennedy, R. Eberhart, and Y. Shi, Swarm Intelligence: Morgan Kaufmann Academic Press, 2001.
[3] Clerc M., "Think Locally, Act Locally - A Framework for Adaptive
Particle Swarm Optimizers", IEEE Journal of Evolutionary Computation,
vol. (submitted), 2002.
[4] Clerc M., "The Swarm and the Queen: Towards a Deterministic and Adaptive Particle Swarm Optimization", Congress on Evolutionary Computation (CEC99), p. 1951-1957, 1999.
[5] M. Clerc, Particle Swarm
Optimization: ISTE (International Scientific and Technical
Encyclopedia), 2006, translated from: M. Clerc, L'optimisation par
essaims particulaires. Versions paramétriques et
adaptatives: Hermès Science, 2005.
From the most recent to the oldest...
[5] Need some chapters of your book *
[4] The Swarm and the Queen *
Maximization with Tribes *
Tribe sizes *
Tribes. Gaussian distribution *
[1] Maths are too difficult *
[3] How do you redefine the neighbourhoods? *
[3] Position and velocity for new particles? *
What do you mean by "fuzzy PSO"? *
[1] I don’t understand at all what you write in page 70 *
[1] I would like a formula for j(r) *
[2] Why do you use j=4.1?
I need
the following chapters of your book
3,4,5,7,9,12,13,14,15,16,17,18
for it is not available in my country and anyway too expensive for me. Please send them to my e-mail box.
Actually you are asking for almost all the book, which has 18 chapters. Unfortunately, it belongs to the publisher. You can buy it on Amazon, although I agree it is a bit expensive. Sorry.
The Swarm and the Queen
I can't see how you go from Equation 12 to Equation 13.
My understanding of equation 12 is that theta(t) is the maximum
distance between any two particles in the population at time t.
However, equation 13 uses the term x(0), which previously in the paper
you were using to mean the position of a "typical" particle at time t=0.
This is what's confusing me.
Answer
As you point out, there are some mistakes in this paper (and the reviewers didn't see them!).
Equ. 9
v(t)=phi*(p-x(t)) instead of v(t)=phi*(p-x(t-1)
Equ. 10
...(1-phi)^(t2+1) instead of ...(1-phi)^t2
and, more important, Equ. 13:
Theta(t)<= max(|p-x|+|p-x'|)
<= 2*max(|p-x(t)|)
<= 2*max(|p-x(0)*(1-phi)^t|)
and you find Equ. 14 by noting that an estimation of the search space
diameter H is about two times the F quantity.
By chance, it is not very important to have the right formula. What
_is_ important is only the fact that this diameter is decreasing.
All your source code is written for minimization. How
should I modify it for maximization problems?
Answer
Normally, you have nothing to change. Let f be the
function to maximize. The easiest way is to minimize 1/f. Or, if the
probability to have f(x) is not null, minimize M-f, where M is bigger
than the maximum f value on the search space (of, course, it means then
you have to know an estimation of this maximum value). Note that this
"trick" is valid for any other optimization method.
When running your program, it seems all tribes tend to become very small, quite often just a single particle. Is it normal?
Answer
Yes. A tribe tends to increase its size only when it is
"bad", and to decrease it when it is "good". So, when the process
convergences, almost all tribes are good and small.
You say Tribes is "parameter free", but there is a parameter when you use the option "Gaussian distribution": the standard deviation. In your program you implicitely set it to 1. Why?
Answer
Using "direct distribution" method, it can be proved that the
process is non divergent (and usually convergent) if the new point has
a probability at least equal to 50% to be inside a hypersphere of radius 
. With the uniform
hyperspherical distribution (UHD), it is automatically sure, but with a
normal distribution, it means that the relative standard
deviation you would have to give is power(1.392,1/D), which rapidly
tends towards 1 when dimension D increases. So, just keep it equal to 1
for a multidimensional problem may be not that bad. Notice, anyway, that
UHD seems to give, on the whole, better result.
It is too difficult for me to understand every thing of the paper, especially part III and part IV. The first two parts are relatively easy. Would you like to explain the original PSO from the math view?
Answer
Well, the math explanation is difficult, so I can't do it just in a few lines. In fact, most of the paper (I mean the math part I have written, not VI, written by Jim Kennedy) details some consequences of equations 3.14, 3.15 and 3.16. In a way, these equations "contain" all the results. You "just" have to chose the set of parameters (a..h) corresponding to the PSO version you want to study.
However, Christian Trelea <trelea@grignon.inra.fr> has recently (2002-09) written a paper "The particle swarm optimization algorithm: convergence analysis and parameter selection" submitted to Information Processing Letters.
In this paper, he simplifies part III and IV for a particular (more classical) class of PSO equations, so you may ask him to send you a copy.
[3] How do you redefine the neighbourhoods?
When generating or killing a particle, do you redefine the neighbourhoods (if the neighbourhood is not equal to the swarm) ? If not, which neighbourhood do you assign the new particle to
Answer
I redefine the neighbourhood, using a "stupid" method ... easy to code ;-)
I say "stupid" for it is depending on how the particles are labelled, which is,theoretically speaking, not a good thing.
Let's suppose you have the swarm (0,1,2,3,5) (the numbers are the labels of theparticles). Here it means particle 4 has already been removed.
For a neighbourhood size of 3 (and a "circular" topology), the neighbourhood of,say, particle 5, is (3,5,0). If I add the particle 6, I simply put it at the end of the list, so you have (0,1,2,3,5,6) and the neighbourhood of 5 is now (3,5,6).
If I remove particle 3, I remove it from the list, so you have (0,1,2,5) and the neighbourhood of 5 is now (2,5,0).
[3] Position and velocity for new particles?
If a new particle is generated, does it receive random initial values for position and velocity or does it inherit anything from the best particle in the neighbourhood ?
Answer
I tried both. The second method if of course more similar to what is done inGAs, but results are not significatively better than pure randomness (I mean sometimes better, sometimes worse).
Note, also, I try to avoid any arbitrary parameter (the next version, caller Tribes, will be completely parameter free), and if you do use inheritance, you have to say something like "x % of the best particle", and it means you have to define x.
What do you mean by "fuzzy PSO"?
I have downloaded the C source code named "fuzzy_pack.c" of a fuzzy PSO and I'm very interested in it, but I don't know what is the main purpose of the fuzzy PSO, Would you like to give me an explanation for it.
Answer
I have written this little fuzzy pack for general
purpose, not
especially for PSO.
As you may have seen on my PSO page ("The old bias..."),
when you use
the classical form rand(0,phi)*(p_i-x) all possible positions are in a
hyperparallelepid, and this implies a bias, for, in fact, it should be a
hypersphere.
The aim of a formula like rand(0,phi)*(p_i-x) is to
choose a point
"around" (p_i-x). A more natural way is to use fuzzy values, and this
is the underlying idea of a fuzzy PSO (from my point of view).
[1] I don’t understand Step 4
In your paper [1] I don’t understand Step 4, in page 67.
Answer
There is a mistake in the published version. Here is the right one.
Step 4. Extension of the complex region and constriction coefficient
In the complex region, according to the convergence
criterion,
in order to get convergence. So the
idea is to find a constriction coefficient depending on 
so that the eigenvalues are true complex numbers for
a large field of values.
This is generally the most difficult step and sometimes needs some intuition. Three pieces of information help us here:
,
So it appears very probable that the same constriction coefficient used for Type 1 will work. First, we try
Equ. 4.15
that is to say 
Equ. 4.16
In this case the common absolute value of the eigenvalues is
Equ. 4.17
which is smaller
than 1 for all values as soon as 
is itself smaller
than 1.
[1] I don’t understandat all what you write in page 70
In [1], I don’t understand at all what
you write in page 70 :
The constriction coefficient c is calculated as shown in Equation 4.15
I think it is not consistent with what you write in Step 4, page 67.
Answer
Right. There is a big mistake in the published version. First, replace Step 4 by the version given in Answer 1. Second, the right version in page 70 is:
The constriction coefficient c is calculated as shown in Equation 4.16:
[1] I would like a formula for j(r)
In [1], in page 68, you give a formula for
the radius of the circular attractor
I see I can compute it as a function of j thanks to the formulas 3.16 and 3.17, but I would like the reciprocal function, I mean j as a function of the radius. It is certainly possible, but I can’t find the formula.
Answer
Note that both c1 and e1can be complex values. It is really difficult, even in some particular cases like PSO Type 1’’ used in part VI.
In this case, and for j=4, you have for example
so you find (you can always suppose y(0)=0 and v(0)=0) :
and then, the corresponding formula 
is horribly complicated.
However, near 4, you have some very good approximations
of 
which are far more sympathetic, like (thanks,
B. Taylor !)
withl=1/8 (if you intend to use PSO near 4.1, you may use l=0.1218, which is a bit better),
which gives the simple formula
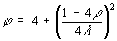
When people use your PSO Type 1’’ (like in [2]), this is always with the coefficient j=4.1. Why ?
Answer
There is a very good reason : it works. In particular Jim Kennedy has done gazillions of tests, with several classical functions, and this value is, globally, the best one (and for each case the optimal value is always very near).
Now, if you are, like me, a theoretician, this is very frustrating, for I have no real proof that this value is indeed an optimal one (there is at least another one smaller than 1), almost not depending on which function you examine.
The qualitative reasoning is the following.
is, the faster is
the convergence towards something (proved)is, the smaller is the envelope of the set of positionsP(T) examined by a particule, for a given number of time stepsT (almost proved), so the smaller is the probability that this somethingindeed is a global optimum (for you have examined just a small part of the search space).
So, there must be a compromise, a
value big enough to have a chance to find the global optimum, and small
enough to have a chance to do it in a reasonable time.
Now, to compute this value, you need to precisely define the relationships "the greater ... the faster", and "the greater ... the smaller".
I already worked on it, thinking it has something to do
with the probabilistic distribution of P(T), which has to
be as near as possible of an uniform one, but in a decreasing search
space. Unsuccessfully for the moment, for I don't find this "magic" 0.1
value for .
After having worked on hyperspherical and independent
Gaussian distributions for Tribes 5.0, my feeling is it has something
to do with 4/0.97725, which is an even better value, and 0.97725 does
have a meaning: for a Gaussian distribution, this is the probability
the value is in the interval average minus/plus 2*standard_deviation.
If you have any idea ...