Maurice Clerc
2003-04-27
Some PSO versions have been specifically designed to cope with Multiobjective Optimization [1,2,3]. As TRIBES is a non-specialized tool, it can't compete with these algorithms, but, as we will see, it is not that bad at all.
Let p1 and p2 be two positions in the search space. Usually, we have just one objective function, and we say that p1 is "better than" p2 iif f(p1)<f(p2). The trick is to define the operator "better than" so that it also works when there are several objective function fi. Of course I used the Pareto's definition: p1 is said to be "better than" p2iif fi(p1)<fi(p2) for all i, and fi(p1)<fi(p2), for at least one i.
It easy to see that this second definition is consistent with the previous one when there is only one objective function. So, I have rewritten the module better_than(p1,p2) according to the second definition. Similarly, I have modified the way the error is calculated. As usually, you give the wanted target S, but the error for a position p is now
![]()
Again, it is consistent with the classical
![]() , so there was nothing else
to change in the program.
, so there was nothing else
to change in the program.
In practice, anyway, we don't know S, so the simplest way is to just set it to zero, and then the stop criterion is the maximum number of position evaluations you allow.
Now, if you want to find several solutions (hopefully near of the Pareto front), you just have to launch several times the program, for the initialization is made at random (with just one particle). As TRIBES converges quite quickly, the best strategy is to run it a lot of times (say 1000), but to allow only a small number of position evaluations for each run (say 20). The strategy set used here is (0,0,0,0), the simplest one, which doesn't try to take into account the "quality" of a particle to choose its own strategy (see the source code for details).
I also added a "cleaning" module that runs after TRIBES itself, which keeps only non dominated solutions. So, if you visualize the result, you more clearly see the front(s). Note that for specific PSO versions, this cleanup is done during the process.
The best specific version I am aware of is
MOPSO, by Coello Coello [1]. So I ran TRIBES (version 4.2) on the examples than
the author has published [1].
Min f1(x1, x2) = x1
Min f2(x1; x2) = g.(1-(x1/g)2-(x1/g).sin(2.pi.x1)), with g=1+10x2, where 0 ≤x1,x2 ≤1
MOPSO generates 200 non dominated points after
4000 evaluations. Figure 1 shows the result with TRIBES after the same number
of evaluations, and Figure 2 an attempt to obtain the same number of non
dominated points.
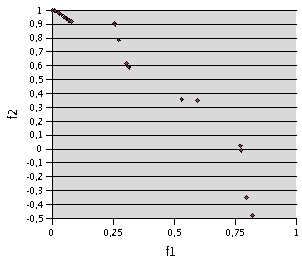
Fig. 1- Problem F1. 4000 evaluations with TRIBES (200 runs with 20 evaluations). Only 22 non dominated points are kept
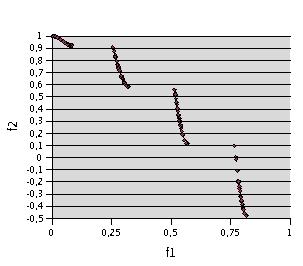
Fig. 2- Problem F1. 34000 evaluations (1700 runs of 20 evaluations) with TRIBES, in order to have about 200 non dominated points (202)
As we can see TRIBES needs 8.5 more evaluations than MOPSO to obtain the same result. Note that, though, the processor time between two evaluations is very short, for almost nothing is done, except sometimes adaptations, as in MOPSO more computations are done (selecting hypercubes, updating the repository, etc.). However, processor times are very difficult to compare, first for different machines are used, and second for TRIBES compute some extra things just for information, and display them or write them on files (for further analysis and visualization).
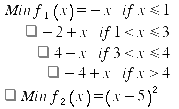 where -5 ≤x≤10.
where -5 ≤x≤10.
MOPSO generates 200 non dominated points after 4000 evaluations.
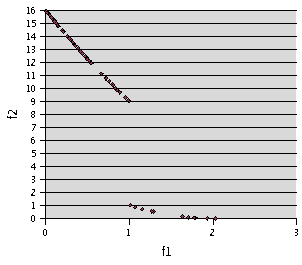
Fig. 3- Problem F2. TRIBES, 200 runs of 20 evaluations
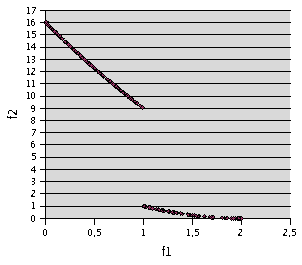
Fig. 4- Problem F2. TRIBES, 900 runs of 10 evaluations. 204 non dominated points
Here TRIBES needs about 2.2 more evaluations
to find a result similar to the one found by MOPSO (see Fig. 4). However,
if you give it exactly the same stop criterion (4000 evaluations), you already
have a pretty good idea of the front (see Fig. 3).
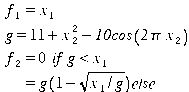
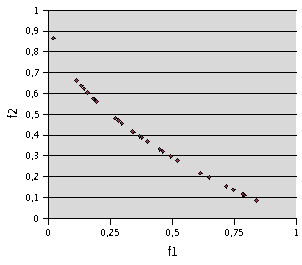
Fig. 5- Problem F3. TRIBES, 160 runs of 20 evaluations
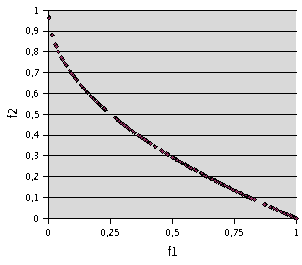
Fig. 6- Problem F3. TRIBES, 1200 runs of 10 evaluations. 194 non dominated points
The good news is that TRIBES can perfectly solve multiobjective problems that are well known to be quite difficult. The bad new is that, not surprisingly, and for a given result quality, it sometimes needs far more position evaluations than the best specific PSO version MOPSO, which seems more or less equivalent to NSGA or PAES. Note that, though, all these specialized algorithms need to be carefully tuned, as TRIBES is completely adaptive and parameter free.
The processor time is still quite reasonable, say a few seconds for the above problems on a 333 MHz personal computer. Note that most of specific algorithms divide the search space into small parts (typically hypercubes, and that is why they are better (Of course, you could do the same with TRIBES, but it means you would have to arbitrary define the number of "cells"). It's OK in 2D, but for such algorithms the processor time will increase like 2D, where D is the number of dimensions. This won't be the case with TRIBES.
So, finally, it was certainly worthwhile to add the multiobjective option to TRIBES, for now any user can solve this kind of problem just by describing it, without the tedious process of finding the "good" parameters. The "price" of this easiness is not very high: just a bit more processor time.
________________________________________________________________________________
[1] Coello Coello C. A., Lechuga M. S., "MOPSO: A Proposal for Multiple Objective Particle Swarm Optimization", Congress on Evolutionary Computation (CEC'2002), Piscataway, New Jersey, 2002, p. 1051-1056.
[2] Hu X., Eberhart R. C., "Multiobjective Optimization Using Dynamic Neighborhood Particle Swarm Optimization",Congress on Evolutionary Computation (CEC'2002), Piscataway, New Jersey, 2002, p. 1677-1681.
[3] Parsopoulos K. E., Vrahatis M. N., "Particle Swarm Optimization Method in Multiobjective Problems", ACM Symposium on Applied Computing (SAC 2002), 2002, p. 603-607.