Particle Swarm Optimization Type 1

Maurice.Clerc@WriteMe.com 1998/11/19

Particle Swarm Optimization Type 1

Parameters and equations

Here we do not study the influence of the swarm size and we are reffering to the PSO form called Type 1, described for each particle and each dimension by an iterative system like:

Equation 1

with

Equation 2

is a constriction coefficient,

v is usually interpreted as the velocity of the particle (along one dimension)

y is the algebraic distance to a temporary objective p (y=p-x, where x is the position of the particle)

j may be seen as an estimation of how much each particle " trust " its neighbours . This is the confidence or social coefficient.

The initial positions and velocities are usually randomly uniformly chosen (between min and max values), but here, on the contrary, we will try different (k,j) values for given " regular " initial conditions . We suppose j is the same constant for all particles and all dimensions. The Equation 2 can also be written

Equation 3

The explicit representations of v and y are then

Equation 4

with

Equation 5

and

Equation 6

(Note that c₁, c₂, e₁ and e₂ are " true " complex numbers if j is smaller than 4, as x(t) and y(t) if t is not an integer).

" Regular " initial conditions

The swarm size is N if the dimensionality D, that is to say the search space is . We study first two kinds of initial conditions (called " init_type " in the maps below). In the first one (init_type=1) all the particles are regularly disposed in and have all the same velocity where . In the second one (init_type=2), the particles are regularly disposed in a few points of . At each of these points we have n particles but the n particles have different velocities (same absolute value but different directions).

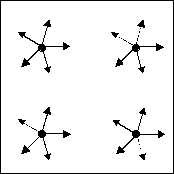
Figure 1. Initial conditions for 20 particles in dimension 2(init_type=2).
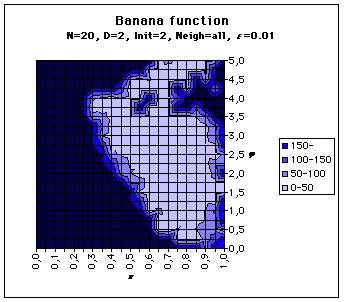
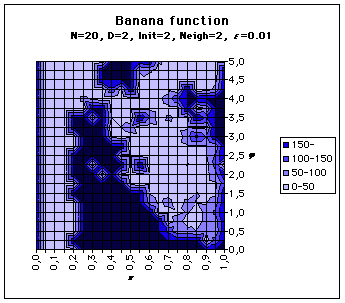
Performances maps

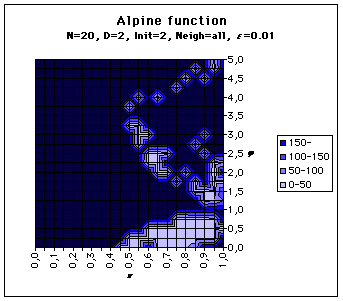
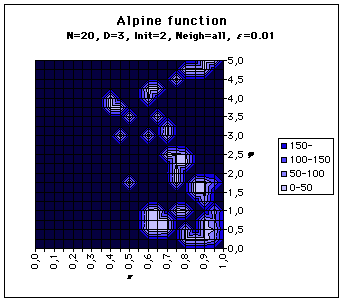
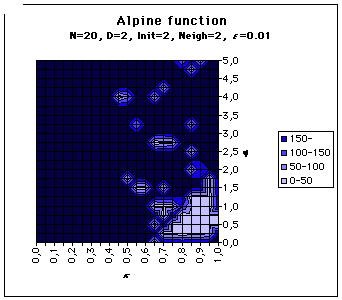
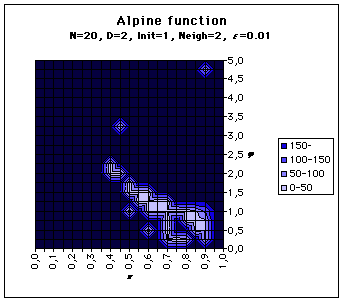
For each (k,j) values we try, the " performance " is here just the convergence time to the solution. It may be infinite. In the maps below, we consider that a convergence time greater than 150 time steps is as bad as an infinite one. We have tried the Rosenbrock’s Banana function and our Alpine function. Also the neighbourood of each particle is either just two others, always the same during the process (Neigh=2) or the whole swarm (Neigh=all).